Apakah nombor rasional? Apakah nombor tidak rasional?

Definisi dan rumus nombor rasional dan tak rasional merupakan pengetahuan penting dalam matematik yang mesti difahami oleh pelajar untuk mempunyai asas matematik yang kukuh. Artikel berikut memperkenalkan kepada anda definisi, sifat dan bentuk matematik nombor rasional dan tidak rasional. Sila rujuk padanya.

Nombor rasional, nombor tak rasional

• Apakah nombor rasional?
  • Pengelasan nombor rasional
  • Mewakili nombor rasional pada garis nombor
  • Tambah dan tolak nombor rasional
  • Darab dan bahagi nombor rasional
  • Nilai mutlak nombor rasional
  • Bandingkan dua nombor rasional
  • Formula untuk mengira kuasa nombor rasional
• Apakah nombor tidak rasional?
  • Konsep nombor tak rasional
  • Sifat nombor tak rasional
• Apakah perbezaan antara nombor rasional dan tidak rasional?
• Hubungan set nombor
• Latihan nombor rasional

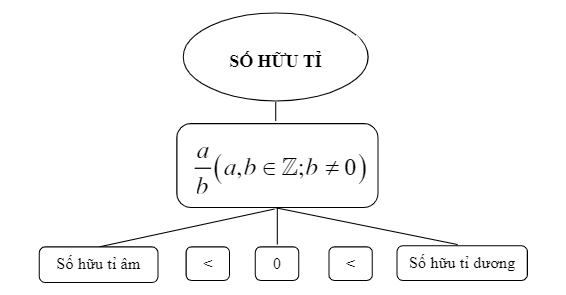
Apakah nombor rasional?

- Nombor rasional ialah set nombor yang boleh ditulis sebagai pecahan (quotient). Iaitu, nombor rasional boleh diwakili oleh perpuluhan berulang tak terhingga.

- Nombor rasional ditulis sebagai , di mana a dan b ialah integer tetapi b mesti berbeza daripada 0.

- ialah set nombor rasional.

=> Set nombor rasional: .

Contohnya: , , … ialah nombor rasional.

• Mana-mana integer a ialah nombor rasional kerana integer a boleh ditulis dalam bentuk .

Sebagai contoh: Kami mempunyai nombor rasional.

Kami ada:

Ulasan: adalah semua nombor rasional.

Pengelasan nombor rasional

Nombor rasional terbahagi kepada dua jenis: nombor rasional negatif dan nombor rasional positif. Secara khusus:

• Nombor rasional negatif: Sertakan nombor rasional kurang daripada 0.
• Nombor rasional positif: Sertakan nombor rasional lebih daripada 0.

Nota: Nombor 0 bukanlah nombor rasional negatif mahupun nombor rasional positif.

alam semula jadi

• Set nombor rasional ialah set boleh dikira.
• Sifat komutatif:
• Harta tambahan dengan 0:
• sifat gabungan:

Mewakili nombor rasional pada garis nombor

- Untuk mewakili nombor rasional pada garis nombor, kami mengikuti faktor berikut:

Langkah 1: Tulis nombor rasional sebagai pecahan

Langkah 2: Bahagikan segmen garisan unit kepada b bahagian yang sama untuk mendapatkan segmen unit baharu iaitu unit lama.

Langkah 3: Nombor rasional diwakili oleh titik A sebagai jarak unit baru dari titik 0.

• A berada di sebelah kiri 0 jika ia adalah nombor negatif.
• A berada di sebelah kanan 0 jika ia adalah nombor positif.

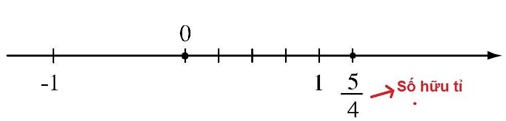
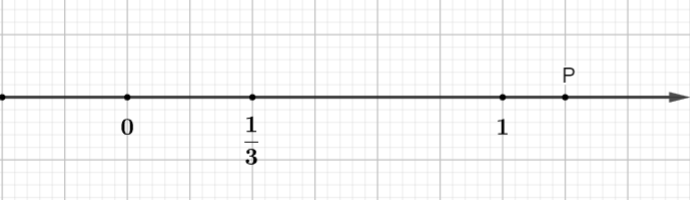
Sebagai contoh: Dalam rajah, titik P mewakili nombor rasional:

Mengarahkan

Segmen garis unit dibahagikan kepada 6 bahagian yang sama (unit baharu ialah 1/6 unit lama)

Titik P terletak pada jarak 7 unit baru dari titik O.

Dan titik P adalah di sebelah kanan titik O jadi P ialah nombor rasional positif.

Jadi P mewakili nombor rasional.

Tambah dan tolak nombor rasional

i) Peraturan menambah dan menolak dua nombor rasional

Kita boleh menambah dan menolak dua nombor rasional x dan y dengan menulisnya sebagai dua pecahan dan kemudian menggunakan peraturan untuk menambah dan menolak pecahan.

Bersama kami kami ada:

ii) Hartanah

- Penambahan nombor rasional mempunyai sifat penambahan pecahan: Komutatif, bersekutu, penambahan dengan 0, penambahan dengan berlawanan.

- Kami ada:

a) Sifat komutatif:

b) Sifat bersekutu:

c) Tambah 0:

d) Tambahkan nombor berlawanan:

iii, Peraturan Peralihan

Apabila memindahkan sebutan dari satu sisi persamaan ke yang lain, kita mesti menukar tanda istilah itu.

Dalam Q kita mempunyai jumlah algebra, di mana kita boleh menukar sebutan, meletakkan kurungan kepada istilah kumpulan secara sewenang-wenangnya seperti jumlah algebra dalam set integer.

• Dengan jika kemudian
• Bersama kami kami ada:

Darab dan bahagi nombor rasional

i) Peraturan untuk mendarab dan membahagi dua nombor nisbah

- Kita boleh mendarab dan membahagi dua nombor rasional dengan menulisnya sebagai pecahan dan kemudian menggunakan peraturan untuk mendarab dan membahagi pecahan.

• Bersama kami kami ada:
• Bersama kami kami ada:

Contohnya:

Darab nombor rasional: 

Bahagikan nombor rasional: 

ii) Hartanah

- Pendaraban nombor rasional juga mempunyai sifat yang sama seperti pendaraban pecahan: Komutatif, bersekutu, pendaraban dengan 1 dan sifat taburan bagi pendaraban atas penambahan.

- Setiap nombor rasional bukan sifar mempunyai songsang.

- Kami ada:

• Sifat komutatif: .
• Sifat bersekutu: .
• Sifat darab dengan 1: .
• Sifat pengedaran: .
• Dengan . Balasan bagi a ialah .

Nilai mutlak nombor rasional

- Nilai mutlak nombor rasional a, dilambangkan dengan , ialah jarak dari titik a ke titik 0 pada garis nombor.

Contohnya:

(Sebab)

(Sebab)

Bandingkan dua nombor rasional

- Dengan mana-mana 2 nombor rasional kita sentiasa ada sama ada atau atau .

- Untuk membandingkan dua nombor rasional kita lakukan perkara berikut:

• Tulis sebagai 2 pecahan dengan penyebut positif yang sama:
• Bandingkan pembilang sebagai integer a, b:

Contohnya: Bandingkan dua nombor rasional: dan

Kami ada:

Kerana ia adalah baik.

Formula untuk mengira kuasa nombor rasional

Formula untuk mengira kuasa nombor rasional yang perlu anda ingat

• Hasil darab dua kuasa dengan asas yang sama:
• Kuasa kuasa
• Kuasa sesuatu produk
• Kuasa hasil bagi

Apakah nombor tidak rasional?

Konsep nombor tak rasional

• Apabila menyebut nombor rasional, seseorang tidak boleh tidak menyebut nombor tidak rasional. Ini ialah nombor yang ditulis dalam bentuk perpuluhan tak terhingga, tidak berulang, dilambangkan dengan .
• Nombor nyata yang bukan nombor rasional tidak boleh diwakili sebagai nisbah.

Contohnya: 3.145248… ialah nombor tidak rasional.

Sifat nombor tak rasional

Set nombor tak rasional ialah set tak boleh dikira.

Contohnya:

Nombor tak rasional: 0.1010010001000010000010000001… (ini ialah perpuluhan tak terhingga tidak berulang)

Bilangan punca kuasa dua: √2 (punca kuasa dua)

Pi (π): 3.14159 26535 89793 23846 26433 83279 50 288…..

Apakah perbezaan antara nombor rasional dan tidak rasional?

• Nombor rasional termasuk perpuluhan berulang tanpa penamat, manakala nombor tak rasional ialah perpuluhan tidak berulang tanpa penamat.
• Nombor rasional hanyalah pecahan, manakala nombor tak rasional mempunyai pelbagai jenis nombor.
• Nombor rasional ialah nombor boleh dikira, manakala nombor tidak rasional ialah nombor tidak boleh dikira.

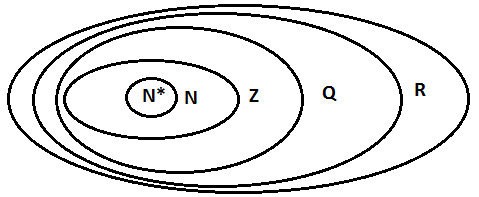
Hubungan set nombor

Simbol set nombor:

• N: Set nombor asli
• N*: Set nombor asli selain 0
• Z: Set integer
• S: Set nombor rasional
• I: Set nombor tak rasional

Kami mempunyai: R = Q ∪ I.

Set N; Z ; Q; R.

Maka hubungan kemasukan antara set nombor ialah: N ⊂ Z ⊂ Q ⊂ R

Latihan nombor rasional

Tingkatan 1: Melakukan pengiraan yang melibatkan nombor rasional

Kaedah penyelesaian: Untuk menyelesaikan latihan melakukan pengiraan yang berkaitan dengan nombor rasional, mula-mula tukar nombor rasional kepada pecahan, kemudian gunakan peraturan pengiraan dengan penambahan, penolakan, pendaraban dan pembahagian nombor rasional.

Contoh: Kira  

Jawapan:

Tingkatan 2: Mewakilkan nombor rasional pada garis nombor

Penyelesaian: Anda perlu menentukan sama ada nombor rasional ialah nombor rasional positif atau nombor rasional negatif, kemudian teruskan dengan langkah seterusnya:

• Jika nombor rasional a/b ialah nombor rasional positif: Pada garis nombor, dalam arah positif, bahagikan panjang 1 unit kepada b bahagian yang sama. Kemudian ambil satu titik pada arah positif paksi Ox, tunjuk bahagian dan tentukan kedudukan nombor rasional a/b.
• Jika nombor rasional a/b ialah nombor rasional negatif: Pada garis nombor, dalam arah negatif paksi, bahagikan panjang 1 unit kepada b bahagian yang sama. Kemudian ambil satu titik pada arah negatif paksi Ox, tunjuk bahagian dan tentukan kedudukan nombor rasional a/b.

Tingkatan 3: Membanding nombor rasional

Penyelesaian: Tukarkan nombor rasional yang diberi kepada pecahan dengan penyebut positif yang sama, kemudian bandingkan pengangkanya. Lebih maju kita boleh bandingkan dengan pecahan perantaraan untuk mencari jawapannya.

Tingkatan 4: Tentukan sama ada nombor rasional adalah negatif, positif atau 0

Kaedah penyelesaian: Untuk menyelesaikan latihan jenis 4, pelajar perlu berdasarkan sifat nombor rasional untuk menentukan sama ada nombor rasional itu negatif, positif atau 0.

Sebagai contoh: Diberi nombor rasional x = (a – 25)/29, tentukan nilai a supaya:

• x adalah negatif
• x positif
• x = 0

Jawapan:

x ialah nombor negatif => (a – 25)/29 < 0=""> a – 25 < 0=""> a <>

x ialah nombor positif => (a – 25)/29 > 0 => a – 25 > 0 => a > 25

x = 0 => (a – 25)/29 =0 0 => a – 25 = 0 => a = 25

Tingkatan 5: Cari nombor rasional dalam selang mengikut syarat yang diberi

Penyelesaian: Jika soalan memerlukan mencari nombor rasional dalam selang masa mengikut syarat yang diberikan, kita perlu meletakkan nombor rasional ke dalam pengangka atau penyebut yang sama untuk mencari jawapannya.

Contoh: Cari nilai m untuk lebih besar daripada dan kurang daripada

Panduan menjawab

Tukarkan pecahan kepada penyebut biasa seperti berikut:

Penyebut biasa: 18

Menurut soalan yang kami ada:

Tingkatan 6: Cari x dengan nombor rasional

Kaedah untuk menyelesaikan masalah matematik: Untuk masalah matematik mencari x dengan nombor rasional, adalah perlu untuk melakukan pengurangan penyebut sepunya dan menukar x kepada satu sisi, dan sebutan yang tinggal kepada 1. Dari situ hitung nilai x

Contohnya: Cari x mengetahui x . (2/ 3) + 5/ 6 = 1/ 8

Jawapan:

x . (2/ 3) + 5/ 6 = 1/ 8

=> x . (2/3) = 1/ 8 + 5/ 6

=> x = 46/ 48 : 2/ 3

=> x = 23 . 3 / 24 . 2

=> 23/16

Borang 7: Cari a supaya ungkapan itu ialah integer

Kaedah untuk menyelesaikan masalah matematik: Untuk masalah mencari a, jika pengangka tidak mengandungi a, kita perlu menggunakan tanda boleh bahagi. Jika pengangka mengandungi a, gunakan tanda boleh bahagi atau pisahkan pengangka dengan penyebut. Jika masalah memerlukan mencari kedua-dua a dan b pada masa yang sama, kumpulan a atau b dan tukarkannya kepada bentuk pecahan untuk pengiraan.

Contoh: Cari integer a dengan keadaan 8/(a – 1) ialah integer

Jawapan:

Keadaan: a – 1 ≠ 0 => a ≠ 1

Biarkan a menjadi integer => 8 boleh dibahagi dengan (a – 1)

=> (a – 1) ialah faktor 8 => U(8) = {-8, -4, -2, -1, 1, 2, 4, 8}

=> (a – 1) = {-8, -4, -2, -1, 2, 4, 8}

=> a = {-7, -3, -1, 0, 3, 5, 9}

Semoga artikel di atas telah membantu anda memahami apa itu nombor rasional, apakah itu nombor tak rasional, jenis nombor rasional, apakah simbol nombor rasional, dan cara mengenal nombor rasional untuk menyelesaikan masalah dengan mudah.

Sebagai tambahan kepada pengetahuan tentang nombor tak rasional dan nombor rasional di atas, anda boleh merujuk beberapa pengetahuan matematik lain seperti pecahan , nombor bercampur , perpuluhan ...