Artikel ini memperkenalkan formula untuk mengira luas dan perimeter rombus dengan tepat. Nantikan!
1. Sifat dan Pengenal Rombus
- Pengenalan
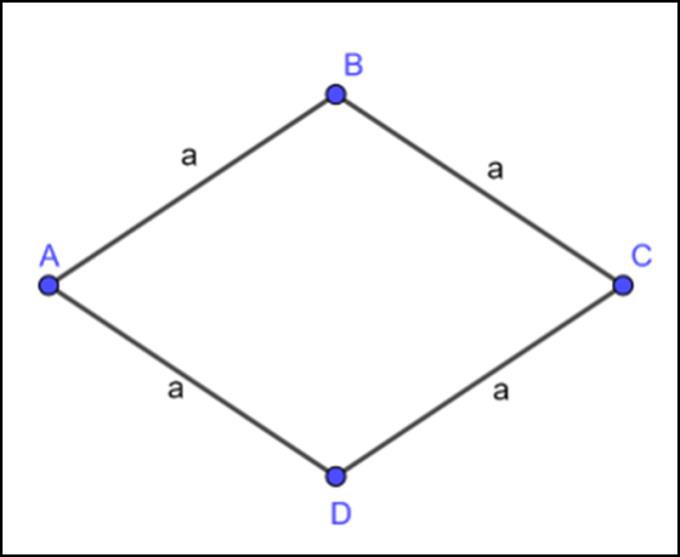
Rombus adalah segiempat dengan empat sisi yang sama. Ia juga merupakan sejenis parallelogram, yang mempunyai dua pasang sisi yang tidak bersebelahan, atau jika dua garis pepenjuru berserenjang antara satu sama lain, ia juga merupakan rombus.
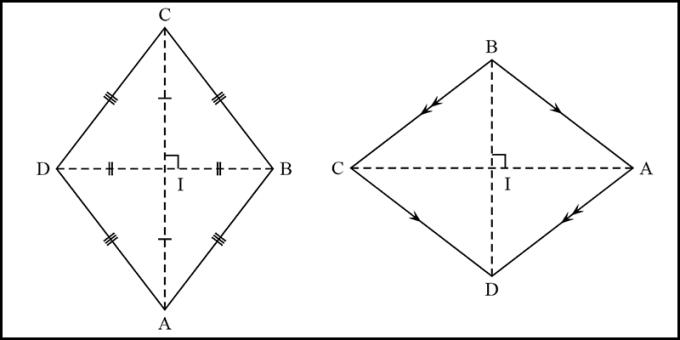
- Hartanah
- Rombus mempunyai semua sifat parallelogram: Bahagian yang berlawanan adalah selari dan sama, sudut sama, garis pepenjuru bersilang pada titik tengah setiap garis.
- Garis diagonal rombus adalah tegak lurus antara satu sama lain.
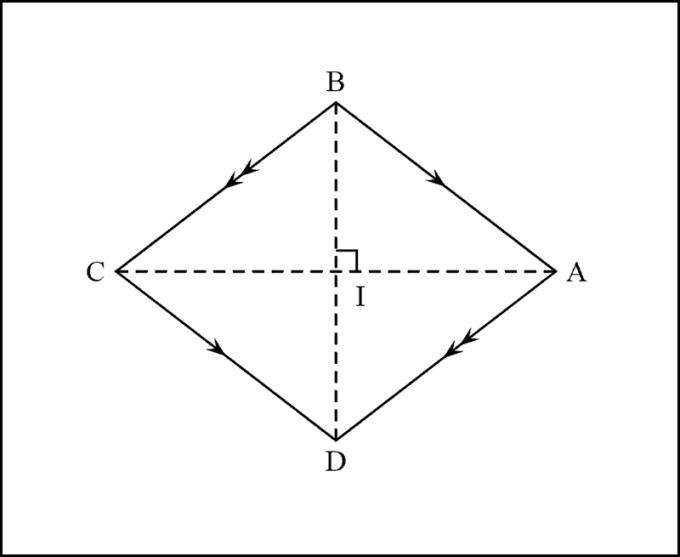
- Tanda Pengenalan
Untuk mengenali rombus, anda perlu menggunakan ciri berikut:
- Kuadrilateral mempunyai 4 sisi yang sama.
- Parallelogram mempunyai 2 sisi bersebelahan yang sama.
- Parallelogram mempunyai 2 garis pepenjuru yang saling tegak lurus antara satu sama lain.
- Parallelogram dengan pepenjuru adalah pembagi sudut.
2. Rumus untuk Mengira Luas Rombus
- Pengenalan
Mengira luas rombus membantu anda mengira kawasan di dalam rombus.
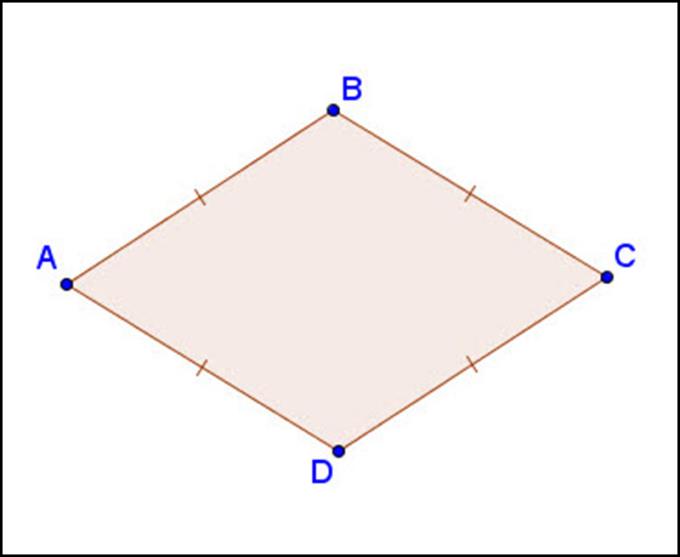
- Rumus
Luas sebuah rombus boleh dikira menggunakan dua cara:
- Separuh daripada hasil darab kedua-dua pepenjuru.
- Hasil darab tinggi ke pangkal yang sesuai.
- Makna Setiap Kuantiti dalam Formula
| Simbol |
Keterangan |
| S |
Kawasan rombus |
| d1, d2 |
Saiz 2 pepenjuru rombus |
| h |
Tinggi rombus |
| a |
Panjang sisi rombus |
- Contoh Pengiraan
Contoh pengiraan luas rombus: Jika panjang pepenjuru adalah d1 = 5cm, dan d2 = 10cm, kita boleh gunakan formula berikut:
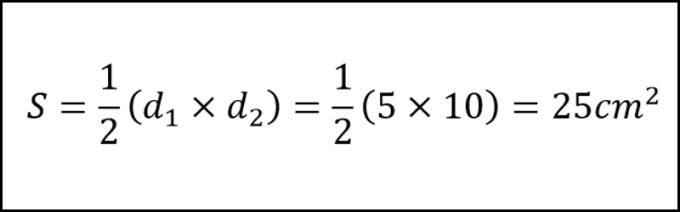
3. Rumus untuk Mengira Keliling Rombus
- Pengenalan
Mengira keliling rombus adalah jumlah panjang keempat sisi rombus.
- Rumus
Keliling rombus adalah:
P = 4a (di mana a adalah panjang satu sisi rombus)
- Makna Setiap Kuantiti dalam Formula
| Simbol |
Keterangan |
| P |
Keliling rombus |
| a |
Panjang salah satu sisi rombus |
- Contoh Pengiraan
Contoh: Hitung keliling rombus dengan panjang sisi . Maka:
P = 5 x 4 = 20cm
4. Kaedah Mengingat Formula untuk Mengira Perimeter dan Luas Rombus
Formula perimeter rombus mudah diingat kerana ia hanya menjumlahkan panjang sisi. Anda hanya perlu mengetahui panjang satu sisi untuk mengira keliling.
Tidak jauh berbeda, untuk luas rombus, anda perlu mengingat dua formula utama.
5. Perhatian Semasa Mengira Luas dan Keliling Rombus
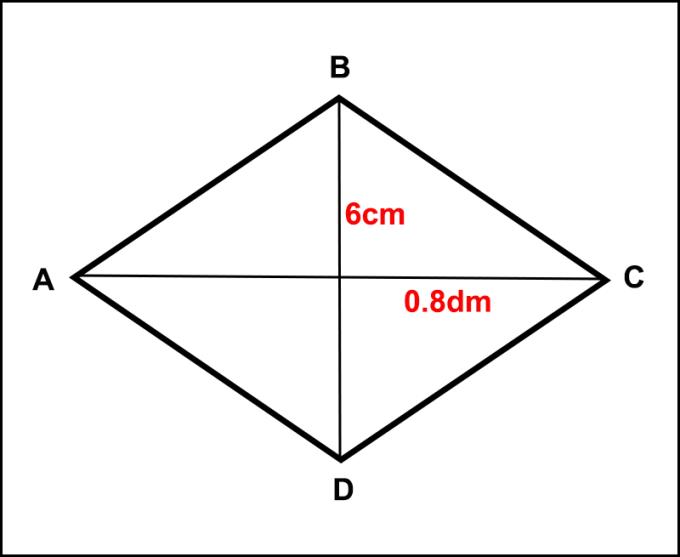
- Pastikan unit kawasan yang digunakan adalah panjang unit + kuasa dua.
- Perhatikan keseragaman unit ketika mengukur panjang pepenjuru, ketinggian, dan sisi sebelum mengira.
Lihat juga:
Demikianlah rumus untuk mengira perimeter dan luas rombus serta kaedah mengingatnya. Terima kasih kerana membaca, dan kami akan berjumpa lagi dalam artikel seterusnya!



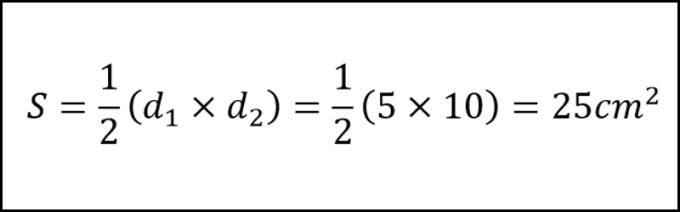








Baba Bear -
Belajar tentang pelbagai bentuk geometri sangat menarik. Saya suka idea tentang membuat model rombus
Hani Cheetah -
Wow, baru perasan betapa pentingnya rumus ni dalam geometri. Dulu, saya ingat rombus hanya bentuk biasa je!
Ali J -
Ini membantu saya dalam praktikal matematik. Saya selalu keliru dengan bentuk rombus dan cara mengiranya
Natasha -
Berapa ramai yang masih ingat cara untuk mengira luas rombus? Hah, saya pasti nak kongsikan kepada kawan
Imran -
Hebat! Sangat berguna untuk pelajar sekolah rendah dan menengah. Saya pun kalau boleh, nak ajar adik saya menggunakan rumus ini
Mira P. -
Akhirnya, saya dapat jawapan yang saya cari! Semoga semua pelajar di luar sana dapat manfaat
Nadia Pet -
Baru minggu lepas belajar tentang ini dalam kelas. Terima kasih untuk maklumat tambahan
Dina & Sari -
Rombus memang bentuk yang cantik! Ada sesiapa yang pernah buat aktiviti kolaj menggunakan bentuk ini
Aira 99 -
Saya rasa topik ini sangat relevan untuk ujian matematik depan. Terima kasih penulis!
Jasmine -
Apa yang menarik tentang geometri adalah kepentingan aplikasinya dalam seni bina. Sangat menarik
Siti Merah -
Saya baru tahu tentang perimeter rombus. Jadi, kita perlu tahu panjang sisi juga ya? Minat nak belajar lebih
Rei 77 -
Mari kita buat kuiz tentang rumus ini! Saya rasa banyak orang akan suka mencabarnya!
Husein -
Perimeter rombus kelihatan rumit tetapi dengan penerangan ini, saya rasa saya boleh lebih faham. Terima kasih!
Yasmin 88 -
Kalau ada contoh soalan yang melibatkan rumus ini, pasti lebih membantu!
Fikri IT -
Saya rasa rumus ini boleh diterapkan dalam projek seni juga! Rombus sangat estetik dalam kad ucapan.
Ravi 90 -
Apakah ada cara mudah untuk mengira luas rombus tanpa perlu ingat rumus? Mungkin ada aplikasi yang membantu?
Diana Merah -
Sangat informatif, terima kasih! Kenapa kita tidak belajar ini lebih awal ya?
Diana KG -
Jangan lupa, aplikasi dalam kehidupan seharian sangat penting! Rombus ada di mana-mana!
Ling Ling -
Cuba buat eksperimen di rumah, potong kertas bentuk rombus. Sangat menarik
Zara 21 -
Apakah ada software yang membantu mengira luas dan perimeter rombus ini? Minta cadangan
Rizky IT -
Baru tujuh bulan belajar, dan semua ini sangat membantu untuk sesi pembelajaran saya. Terima kasih banyak
Rizqi A -
Konten ini sangat penting untuk pelajar! Mungkin perlu tambahkan lebih banyak contoh, ya?
Farah L -
Menarik! Saya sering merujuk kepada artikel-artikel seperti ini. Sangat membantu untuk belajar matematik dengan cara yang ringan
Sofia Lala -
Rumus ini sangat berguna! Saya suka matematik, tapi geometri kadangkala mencabar sedikit
Farid R -
Pernah tak anda buat rumus rombus ini dalam bentuk graf? Keren untuk visualisasi
Kamal -
Setuju dengan penulis tentang pentingnya memahami bentuk geometri. Ini akan membantu banyak pelajar di luar sana
Leia -
Rumus untuk luas rombus memang penting. Banyak orang terlepas pandang perkara ini dalam pembelajaran mereka!
Rina Sweets -
Adakah semua rombus mempunyai perimeter yang sama jika sisi-sisinya berbeza? Minta penjelasan
Aliya -
Saya suka bagaimana informasi ini disusun. Sangat mudah untuk pemahaman!
Eka -
Siapa sangka geometri boleh jadi semudah ini? Ternyata belajar dengan cara yang betul itu penting
Aiman -
Terima kasih untuk rumus ini! Sangat membantu dalam menjelaskan luas rombus kepada pelajar saya.
Muhammad J -
Wow, baru teringat tentang belajar matapelajaran ini di sekolah. Terima kasih kerana membuatnya menarik semula
Sam 04 -
Saya suka bagaimana artikel ini membincangkan asas-asas rumus. Sangat jelas dan mudah difahami!
James H. -
Saya ingin tahu lebih lanjut tentang aplikasi praktikal rumus ini! Ada sesiapa yang pernah menggunakannya dalam pembangunan?