Mari belajar tentang formula pengiraan luas sisi, jumlah luas dan ketinggian silinder untuk digunakan dalam kajian dan kehidupan harian.
Jadual Kandungan
Bagaimana untuk mengira luas silinder
Luas silinder termasuk luas sisi dan jumlah luas.
Anda boleh memasukkan ketinggian dan jejari silinder ke dalam jadual di bawah untuk mengetahui luas sisi dan jumlah luas silinder.
Formula untuk mengira luas sisi silinder
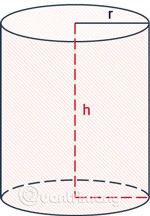
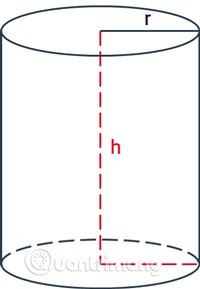
Kawasan sisi silinder hanya merangkumi kawasan permukaan sekeliling yang mengelilingi silinder, tidak termasuk luas dua tapak.
Formula untuk mengira luas sisi silinder ialah lilitan bulatan asas didarab dengan ketinggian.
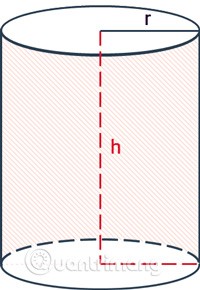 |
Di sana:
- Sekitar adalah kawasan sekitar.
rialah jejari silinder.hialah ketinggian, jarak antara dua tapak silinder.
|
Contoh: 1
Sebuah silinder bulat mempunyai jejari tapak r = 5 cm, tinggi h = 7cm. Kira luas sisi silinder menegak.
Penyelesaian: Luas permukaan silinder bulat: Sxq = 2.π.rh = 2π.5.7 = 70π = 219.8 (cm2).
Contoh: 2
Diberi segi empat sama ABCD dengan sisi 2a. Biarkan O dan O' masing-masing ialah titik tengah sisi AB dan CD. Apabila memutar petak itu di sekeliling paksi OO', kita mendapat silinder berputar. Kira luas permukaan silinder berputar.
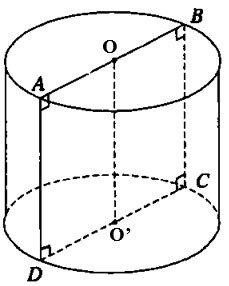
Penyelesaian:
Jejari bulatan tapak ialah r= CD= a
Ketinggian silinder ialah h= OO'= AD=2a
Jadi luas sisi silinder ialah Sxq = 2πrh = 2π.a.2a =4a2π
Formula untuk mengira jumlah luas silinder
Jumlah kawasan dikira sebagai magnitud keseluruhan ruang yang diduduki oleh rajah, termasuk luas sisi dan luas dua tapak bulat.
Formula untuk mengira jumlah luas silinder ialah luas sisi ditambah luas dua tapak.
Contoh 1 : Kira jumlah luas silinder dengan tapak 3 dan ketinggian 5.
Penyelesaian:
Jumlah kawasan ialah Stp= Sxq + 2Sd = 2πr(r+h) = 2π.3(3+5) =48π
Kira ketinggian silinder itu
Ketinggian silinder ialah jarak antara dua tapak silinder.
Kira ketinggian silinder apabila mengetahui jumlah luas dan jejari tapak
Contohnya: Diberi sebuah silinder dengan jejari tapak R = 8cm dan jumlah luas 564π cm2 . Kira ketinggian silinder itu.
Hadiah:
Kami ada
Kira ketinggian silinder apabila mengetahui luas sisi
=>
Formula untuk mengira jejari tapak silinder
1. Formula untuk mengira lilitan bulatan; kawasan bulatan
Bulatan mempunyai lilitan C=2πr
=>
Bulatan dengan tapak mempunyai luas S=πr2
=>
Contohnya. Kira jejari tapak silinder dalam kes berikut:
a. Lilitan bulatan tapak ialah 6π
b. Luas tapak ialah 25π
Penyelesaian:
a. Jejari bulatan tapak ialah
b. Jejari bulatan tapak ialah
2. Tapak ialah bulatan yang tertulis dalam poligon
- Ditulis dalam mana-mana segi tiga: dengan S ialah luas segi tiga dan p ialah separuh perimeter
- Ditulis dalam segi tiga sama sisi: sisi
- segi empat sama bertulis:
Contoh 1 . Diberi sebuah silinder yang ditulis dalam kubus dengan tepi a. Hitung jejari silinder itu.
Jejari silinder ialah:
Contoh 2 . Diberi sebuah prisma sekata ABC.A'B'C' dengan , isipadu yang dihadkan di sekeliling silinder. Hitung jejari silinder itu.
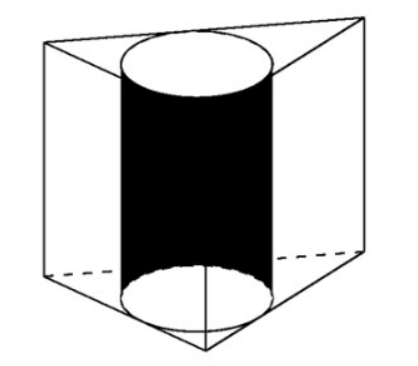
Isipadu prisma itu ialah
Tapak prisma sekata ialah segi tiga sama sisi, jadi => sisi
Oleh itu, jejari tapak silinder ialah:
3. Tapak ialah bulatan yang mengelilingi poligon.
Terhad dalam mana-mana segi tiga:
Di sana:
- a, b, c ialah panjang tiga sisi segitiga itu
- p ialah separuh perimeter segi tiga:
Lilitan segi tiga tegak: hipotenus
Pinggir segi tiga sama sisi: sisi
Lilitan segi empat sama: sisi
Contohnya:
Kira jejari tapak silinder yang mengehadkan piramid biasa S.ABC dalam kes berikut:
a. ABC ialah segi tiga tegak di A dengan AB = a dan AC = a√3
b. ABC mempunyai AB= 5; AC= 7; BC=8
Hadiah:
a. Hipotenus
Kerana ABC ialah sudut tegak di A, jejari R=0.5.BC=a
b. Separuh perimeter segi tiga ABC ialah
Apakah silinder bulat?
Silinder bulat ialah silinder dengan dua tapak bulat yang sama selari antara satu sama lain.
Silinder digunakan agak biasa dalam masalah geometri daripada asas kepada kompleks, di mana formula untuk mengira luas dan isipadu silinder sering digunakan secara berbeza. Jika anda sudah tahu cara mengira luas dan lilitan bulatan, anda boleh dengan mudah menyimpulkan formula untuk mengira isipadu, luas sisi, dan jumlah luas silinder.
Formula untuk mengira luas keratan rentas silinder
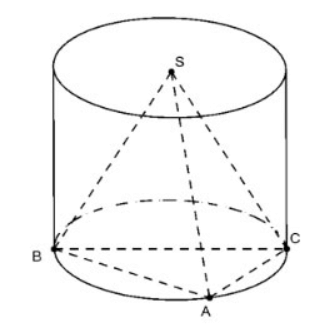
Potong silinder mengikut satah (P) melalui paksi
- Keratan rentas yang terhasil ialah segi empat tepat.
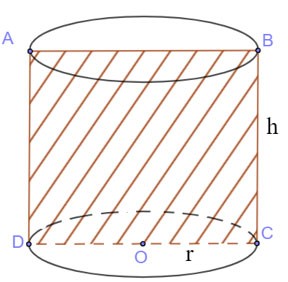 |
Luas keratan rentas:
SABCD = BC.CD =2r.h
|
Potong silinder dengan satah (P) selari dengan dan jarak x dari paksi
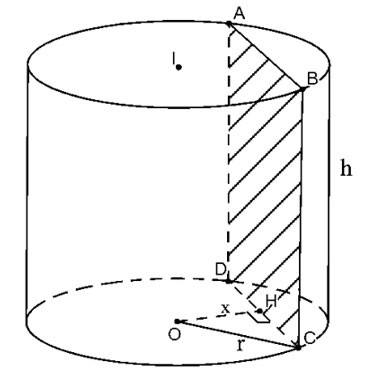 |
Keratan rentas yang terhasil ialah segi empat tepat ABCD seperti yang ditunjukkan di atas.
Biarkan H ialah titik tengah CD, kita mempunyai OH ⊥ CD=>
Oleh itu luas keratan rentas
|
Potong silinder mengikut satah (P) tidak berserenjang dengan paksi tetapi potong semua penjana silinder
 |
Keratan rentas yang terbentuk ialah bulatan berpusat O' dan jejari O'A'=r
Luas keratan rentas: S= πr2
|
Potong silinder mengikut satah (P) tidak berserenjang dengan paksi tetapi potong semua penjana silinder.
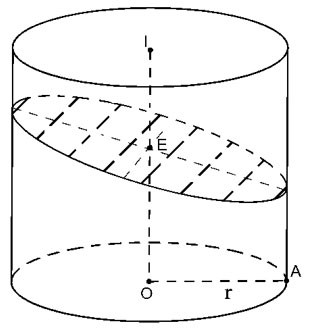 |
Keratan rentas yang terhasil ialah Ellipse (E) dengan paksi kecil 2r => a=r
Paksi besar sama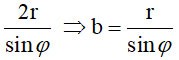
dengan 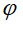 ialah sudut antara paksi OI dan (P) ialah sudut antara paksi OI dan (P)
Oleh itu luas S= π. ab=
|
Contoh pengiraan luas silinder
Pelajaran 1 :
Luas sisi silinder mempunyai lilitan tapak bulat 13cm dan tinggi 3cm.
Hadiah:
Kami mempunyai: lilitan bulatan C = 2R.π = 13cm, h = 3cm
Jadi luas sisi silinder ialah:
Sxq = 2πr.h = Ch = 13.3 = 39 (cm²)
Pelajaran 2 : Diberi sebuah silinder dengan jejari bulatan tapak 6cm, manakala ketinggian dari tapak ke bahagian atas silinder ialah 8cm tebal. Berapakah luas sisi dan jumlah luas silinder?
Hadiah
Mengikut formula, kita mempunyai separuh bulatan asas r = 6 cm dan ketinggian silinder h = 8 cm. Oleh itu, kami mempunyai formula untuk mengira luas sisi silinder dan jumlah luas silinder seperti berikut:
Luas permukaan silinder = 2 x π xrxh = 2 x π x 6 x 8 = ~ 301 cm²
Jumlah luas silinder = 2 Π x R x (R + H) = 2 X π x 6 x (6 + 8) = ~ 527 cm²
Pelajaran 3 : Sebuah silinder mempunyai jejari tapak 7cm dan luas sisi 352cm2.
Kemudian, ketinggian silinder ialah:
(A) 3.2 cm; (B) 4.6cm; (C) 1.8 cm
(D) 2.1cm; (E) Keputusan lain
Sila pilih hasil yang betul.
Penyelesaian: Kami ada
Jadi, jawapan E adalah betul.
Pelajaran 4 : Ketinggian silinder adalah sama dengan jejari bulatan tapak. Luas sisi silinder ialah 314 cm2. Kira jejari bulatan tapak dan isipadu silinder (bulatkan hasilnya kepada dua tempat perpuluhan).
Hadiah:
Luas sisi silinder ialah 314cm2
Kami mempunyai Sxq = 2.π.rh = 314
Di mana r = h
Jadi 2πr² = 314 => r² ≈ 50 => r ≈ 7.07 (cm)
Isipadu silinder: V = π.r2.h = π.r3 ≈ 1109.65 (cm³).
Semoga artikel di atas telah membantu anda memahami pengetahuan asas dan lanjutan tentang silinder, cara mengira jumlah luas dan luas sisi silinder.









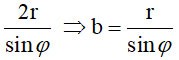
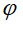 ialah sudut antara paksi OI dan (P)
ialah sudut antara paksi OI dan (P)