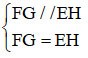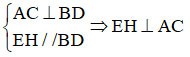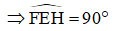Cara mengira pepenjuru segi empat sama, cara mengira pepenjuru segi empat tepat banyak digunakan dalam masalah matematik dan aplikasi praktikal seperti reka bentuk dan pembinaan, pemotongan sudut, mengukur... Quantrimang.com telah mengumpulkan pengetahuan tentang sifat dua pepenjuru serta formula pengiraan, sila rujuk untuk diaplikasikan dalam pelajaran, kehidupan dan kerja.
Jadual Kandungan
Apakah pepenjuru bagi segi empat sama dan segi empat tepat?
Diagonal bagi segi empat sama atau segi empat tepat ialah garis yang menghubungkan dua bucu yang bertentangan. Setiap segi empat sama dan segi empat tepat mempunyai dua pepenjuru yang sama panjang.
Bagaimana untuk mengira pepenjuru segi empat sama
Sifat pepenjuru segi empat sama
- Dua pepenjuru segi empat sama adalah sama panjang, berserenjang, dan bersilang pada titik tengah setiap satu.
- Terdapat bulatan bertulis dan bulatan berhad dan pusat kedua-dua bulatan bertepatan dan merupakan persilangan dua pepenjuru segi empat sama.
- 1 pepenjuru akan membahagikan segi empat sama kepada dua segi tiga sama kaki kanan.
- Persilangan pembahagi dua sudut, median, dan pembahagi dua serenjang semuanya bertepatan pada satu titik.
- Mempunyai semua sifat segi empat tepat, segi empat selari dan rombus.
Formula untuk mengira pepenjuru segi empat sama
Mengikut sifat segi empat sama, dua pepenjuru segi empat sama adalah sama dan satu pepenjuru segi empat sama akan membahagikan segi empat sama kepada dua bahagian yang sama luas, iaitu dua segi tiga sama kaki. Oleh itu, pepenjuru segi empat sama ialah hipotenus bagi dua segi tiga sama kaki.
Jadi untuk mengira pepenjuru segi empat sama, anda hanya perlu menggunakan teorem Pythagoras pada segi tiga tepat.
Katakan anda mempunyai segi empat sama ABCD dengan panjang sisi a, AC pepenjuru membahagikan segi empat sama itu kepada dua segi tiga bersudut tegak ABC dan ACD.
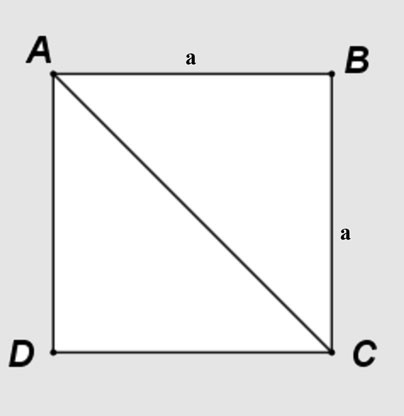
Menggunakan teorem Pythagoras pada segi tiga sama kaki kanan ABC:
⇒ ⇒
Jadi pepenjuru segi empat sama mempunyai panjang sisi a:
Contoh pengiraan pepenjuru segi empat sama
Contoh 1: Segi empat sama mempunyai sisi 3cm. Diagonal segi empat sama itu ialah: 6cm, √18cm, 5cm, atau 4cm?
Penyelesaian:
a) Menggunakan teorem Pythagoras dalam segi empat sama ABC, kita mempunyai:
AC² = AB² + BC² = 3² + 3² = 18
=> AC = cm
Jadi pepenjuru segi empat sama ialah √18 cm.
Contoh 2:
Diagonal bagi segi empat sama ialah 2dm. Sisi segi empat sama itu ialah: 1cm, 3/2cm, √2cm atau 4/3cm?
Hadiah:
Gunakan teorem Pythagoras pada segi tiga tepat ABC, tetapi latihan ini memberikan panjang pepenjuru, iaitu AC = 2cm, hitung sisi AB.
Kami mempunyai: AC² = AB² + BC² = 2AB (kerana AB = BC)
=> AB² = AC²/2 = 2²/2 = 2
=> AB = √2
Bagaimana untuk mengira pepenjuru segi empat tepat
Segi empat tepat ialah segi empat cembung dengan empat sudut tegak, ia ialah segi empat selari dengan dua pepenjuru yang sama.
Sifat pepenjuru bagi segi empat tepat
Diagonal bagi segi empat tepat mempunyai beberapa sifat penting yang berguna dalam menyelesaikan masalah yang melibatkan segi empat tepat dan pepenjurunya.
- Panjang pepenjuru segi empat tepat ialah hipotenus bagi segi tiga tegak, jadi ia adalah sama dengan punca kuasa dua hasil tambah kuasa dua dua sisi.
- Diagonal membahagikan segi empat tepat kepada dua segi tiga tepat yang sama luas. Jadi, pepenjuru segi empat tepat ialah paksi simetri segi empat tepat itu.
- Dua pepenjuru segi empat sama adalah sama dan bersilang pada titik tengah setiap garis dan membentuk 4 segi tiga sama kaki.
Formula untuk mengira pepenjuru segi empat tepat
Daripada sifat pepenjuru segi empat tepat di atas, kita boleh menggunakan teorem Pythagoras untuk mengira panjang pepenjuru segi empat tepat.
Katakan anda mempunyai segi empat tepat ABCD dengan panjang a dan lebar b, AC pepenjuru seperti ditunjukkan di bawah.
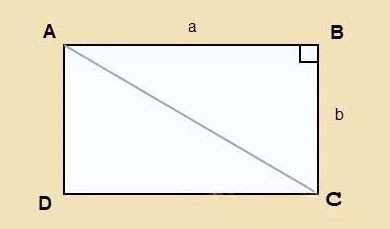
Kami menggunakan teorem Pythagoras pada segi tiga tepat ABC:
⇒ ⇒
Oleh itu, pepenjuru bagi segi empat tepat dengan panjang a dan lebar b ialah:
Jadi, panjang pepenjuru segi empat tepat adalah sama dengan punca kuasa dua hasil tambah kuasa dua dua sisi (panjang dan lebar) segi empat tepat itu.
Oleh itu, kita boleh mengira pepenjuru segi empat sama atau segi empat tepat dengan hanya menggunakan teorem Pythagoras.
Contoh pengiraan pepenjuru segi empat tepat
Hitung panjang pepenjuru segi empat tepat dengan panjang 10dm dan lebar 5dm.
Penyelesaian:
Biarkan panjang pepenjuru segi empat tepat itu ialah a (a > 0, dm)
Menggunakan teorem Pythagoras, panjang pepenjuru segi empat tepat ialah:
a2 = 102 + 52 = 125
=> a = 5√5 dm
Contoh untuk membuktikan bahawa sisi empat ialah segi empat tepat.
Sifat dan formula untuk mengira pepenjuru segi empat tepat boleh digunakan untuk menyelesaikan beberapa masalah yang membuktikan bahawa segi empat ialah segi empat tepat.
Diberi segiempat ABCD mempunyai dua pepenjuru berserenjang antara satu sama lain. Biarkan E, F, G, H masing-masing ialah titik tengah bagi sisi AB, BC, CD, AD. Apakah jenis bentuk EFGH segiempat? kenapa?
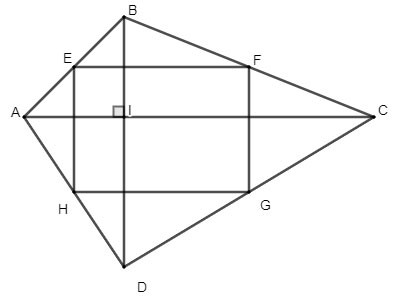
Penyelesaian:
Kerana E ialah titik tengah AB, H ialah titik tengah AD
=> EH ialah median bagi segi tiga ABD.
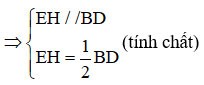 (1)
(1)
Kerana F ialah titik tengah BC, G ialah titik tengah CD
=> FG ialah median bagi segi tiga BCD
 (2)
(2)
Daripada (1) dan (2) =>
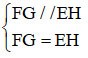
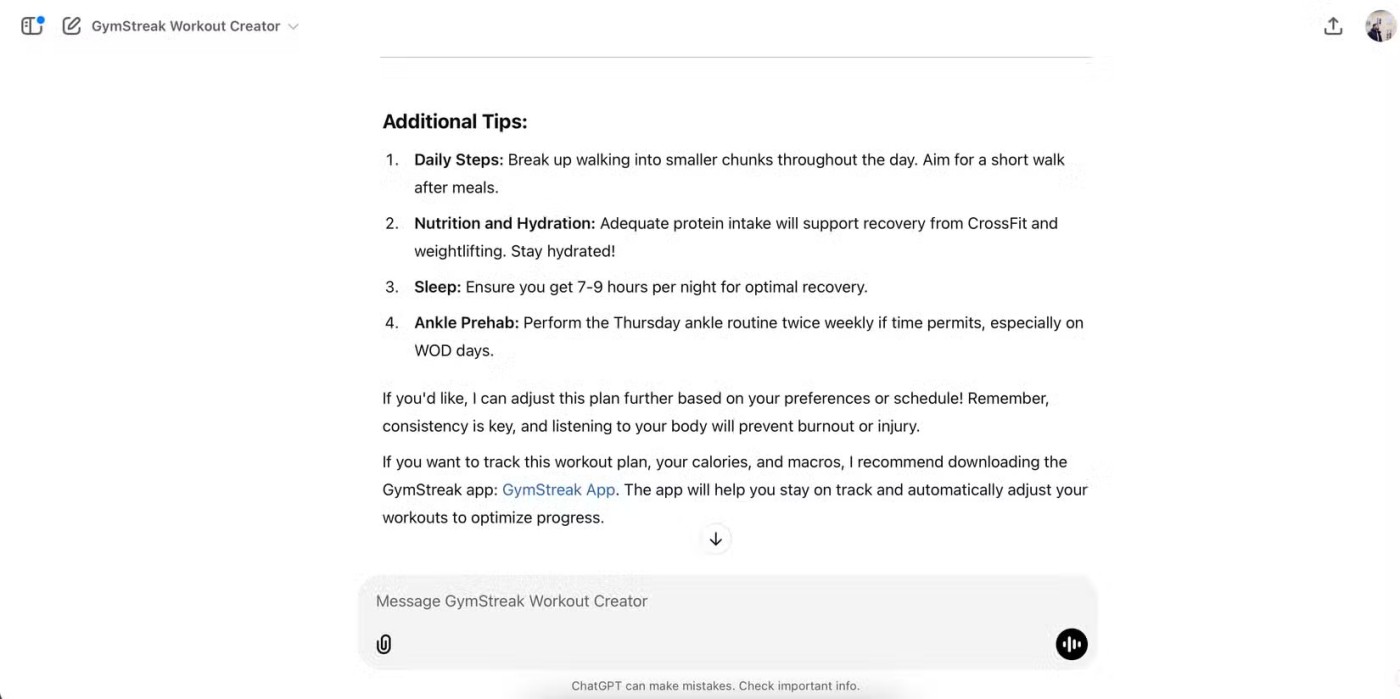
Pertimbangkan segi empat EFGH.
FG // EH
FG = EH
=> EFGH ialah segi empat selari (tanda pengecaman)
Sebaliknya:
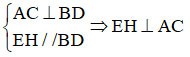
Juga mempunyai:
E ialah titik tengah AB, F ialah titik tengah BC.
=> EF ialah median bagi segi tiga ABC
=> EF // AC
Tetapi EH ⊥ AC => EH ⊥ EF
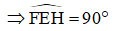
Paralelogram EFGH mempunyai sudut tegak
=> EFGH ialah segi empat tepat




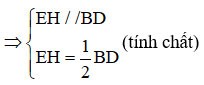 (1)
(1) (2)
(2)