Formula untuk mengira luas permukaan dan isipadu sfera

Mari belajar dan semak semula formula untuk mengira luas permukaan dan isipadu sfera dengan Quantrimang.com dalam artikel di bawah.

Jadual Kandungan

• Apakah sfera?
  • Apakah sfera?
• Formula untuk mengira luas permukaan dan isipadu sfera
  • Formula untuk mengira luas permukaan sfera
  • Formula untuk mengira isipadu sfera:
• Formula untuk mengira jejari sfera
  • Sfera yang mengelilingi piramid mempunyai sisi yang berserenjang dengan tapak.
  • Tetrahedron segi empat sama (ini adalah kes khas formula 1)
  • Prisma tegak mempunyai tapak yang merupakan poligon bertulis.
  • Formula untuk tetrahedron yang bucunya ialah bucu prisma tegak
  • Formula untuk mengira jejari sfera bagi piramid dengan muka sisi berserenjang dengan tapak
• Contoh pengiraan luas permukaan dan isipadu sfera

Apakah sfera?

Sfera ialah lokus titik yang sama jarak dari titik tetap O rdalam ruang 3 dimensi. Titik O dipanggil pusat dan jaraknya rdipanggil jejari sfera.

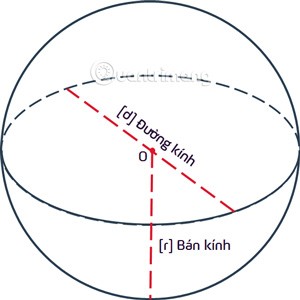
Apakah sfera?

Sfera ialah satu set titik yang terletak di dalam sfera dan sfera dipanggil sfera atau sfera dengan pusat O dan jejari r = OA.

Formula untuk mengira luas permukaan dan isipadu sfera

Formula untuk mengira luas permukaan sfera

Luas permukaan sfera adalah empat kali luas bulatan besar, iaitu empat kali pemalar Pi didarab dengan kuasa dua jejari sfera itu.

Formula untuk mengira isipadu sfera:

Isipadu sfera, juga dikenali sebagai isipadu sfera, dikira dengan mendarab tiga perempat Pi dengan kubus jejari sfera.

Di sana:

• Sialah luas permukaan sfera
• Vialah isipadu sfera
• rialah jejari sfera/sfera
• dialah sfera/sfera

Formula untuk mengira jejari sfera

Sfera yang mengelilingi piramid mempunyai sisi yang berserenjang dengan tapak.

• Rd ialah jejari tapak.
• h ialah panjang sisi yang berserenjang dengan tapak.

Contohnya : Diberi piramid S.ABCD dengan tapak segi empat tepat dengan AB = 3a, BC = 4a, SA = 12a dan SA berserenjang dengan tapak. Hitung jejari R bagi sfera yang mengepung piramid S.ABCD.

Penyelesaian: Kami ada

Jadi

Tetrahedron segi empat sama (ini adalah kes khas formula 1)

Bongkah segi empat sama OABC mempunyai OA, OB, OC, berserenjang antara satu sama lain dan mempunyai:

Contohnya:

Tetrahedron OABC mempunyai OA, OB, OC, saling berserenjang dan mempunyai jejari sfera terhad sebanyak . Isipadu terbesar tetrahedron OABC

Penyelesaian : Kami ada

Sebaliknya kita ada:

Menurut ketidaksamaan AM - GM yang kami ada:

Prisma tegak mempunyai tapak yang merupakan poligon bertulis.

Di sana:

• Rd ialah jejari tapak
• h ialah panjang sisi.

Contoh 1: Diberi satu sfera jejari R yang mengehadkan kubus sisi a. Manakah antara pernyataan berikut adalah benar?

A.

B.

C.

D.

Penyelesaian: Kami ada

Jadi, jawapannya ialah C.

Formula untuk tetrahedron yang bucunya ialah bucu prisma tegak

Tetrahedron (H1) mempunyai bucu yang merupakan bucu prisma menegak (H2), maka:

Formula untuk mengira jejari sfera bagi piramid dengan muka sisi berserenjang dengan tapak

Di mana R, d ialah jejari tapak; a, x masing-masing ialah panjang persilangan muka sisi dan tapak, sudut di bahagian atas muka sisi memandang ke bawah pada tapak.

Atau anda boleh menggunakan formula

Di mana: Rb ialah jejari terhad muka sisi dan a ialah panjang persilangan muka sisi dan tapak.

Contohnya: 

Diberi piramid S.ABCD dengan tapak segi empat sama, segi tiga sama SAD dengan sisi √2a dan terletak dalam satah berserenjang dengan tapak. Hitung jejari R bagi sfera yang mengepung piramid S.ABCD.

A.

B.

Penyelesaian: Kami ada

Jadi jawapan yang betul ialah B.

Contoh pengiraan luas permukaan dan isipadu sfera

Pelajaran 1 : Diberi bulatan dengan lilitan 31.4 cm. Kira isipadu sfera dengan jejari sama dengan jejari bulatan yang diberi.

Hadiah:

Lilitan bulatan C = 2πr = 31.4 cm

=> Jejari r = C/2π = 5 cm

Isipadu sfera yang diberi ialah:

V = ⁴⁄₃πr³ = 4/3.3.14.(5)³ = 523.3 cm³

Pelajaran 2 : Kira isipadu sfera dengan diameter d = 4 cm.

Hadiah:

Jejari r = d/2 = 2 cm

Isipadu sfera ialah:

V = ⁴⁄₃πr³ = 4/3.3.14.(2)³ = 33.49 cm³

Pelajaran 3 :

Biarkan bulatan berdiameter 4a berputar mengelilingi diameternya. Berapakah isipadu pepejal yang berputar itu?

Penyelesaian: Diberi bulatan dengan diameter 4a berputar mengelilingi diameternya, kita mendapat sfera dengan diameter 4a atau jejari R = 2a.

Isipadu sfera ialah:

Pelajaran 4 :

Sfera dengan jejari R√3 mempunyai luas:

A. 4√3πR2

B. 4πR2

C. 6πR2

D. 12πR2

Penyelesaian: Guna formula: S = 4πR2

Luas permukaan sfera dengan jejari R√3 ialah: S = 4π(R√3)2 = 12πR2

Jadi jawapannya ialah D.

Dua formula pendek tetapi untuk mengingati mereka untuk masa yang lama agak sukar. Tandai halaman artikel dan bukanya apabila anda memerlukannya. Semoga artikel ini bermanfaat kepada anda.

Sebagai tambahan kepada formula untuk mengira luas permukaan dan isipadu sfera di atas, anda juga boleh merujuk kepada formula untuk mengira luas beberapa bentuk asas lain seperti segi tiga , segi empat tepat dan segi empat selari. ..